Many years ago I bought a box of Christmas baubles. The baubles were arranged in a simple cubic lattice. I was not happy because the box was almost as empty as it was full.

The arrangement of the baubles means that 48% of the box is empty, and only 52% is bauble. If a hexagonal prism box was used, and a hexagonal close-packed lattice was chosen for stacking the baubles, just 26% of the space would be empty, and 74% would be bauble. That’s 42% more bauble!
Where did those numbers come from? Let’s start with the simple cubic lattice.
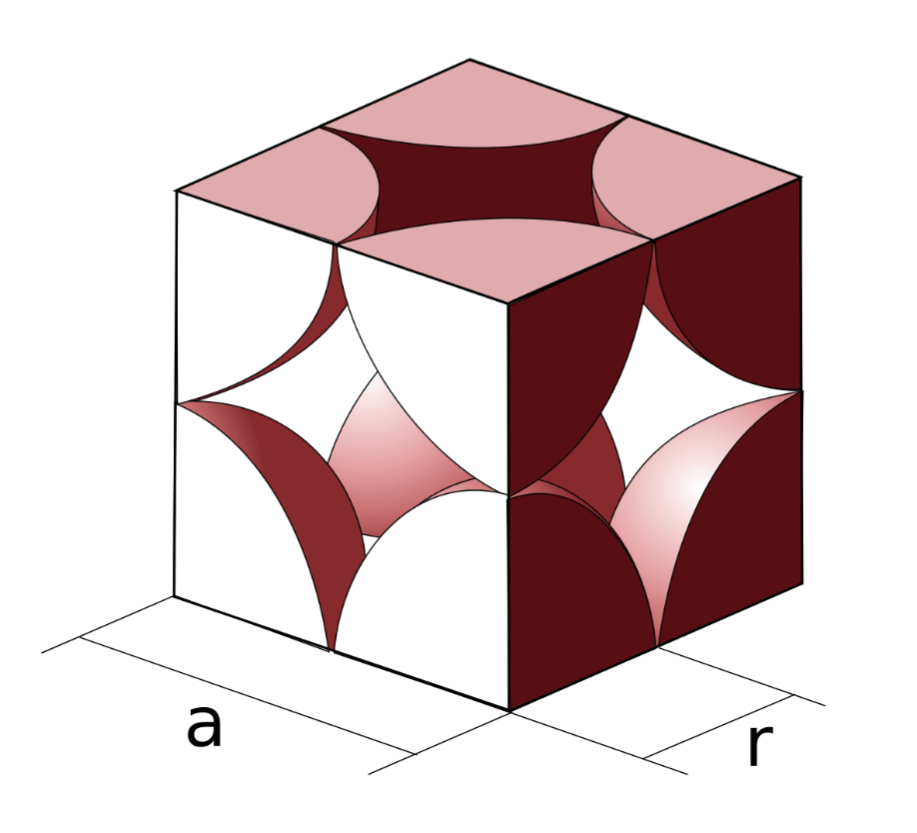
The volume V=a³ fits 8× ⅛th of a sphere where the radius r is ½a. The volume of a sphere v=4πr³/3, or v=4πa³/(3×8) or v=4πV/24 or v/V=π/6=0.524. That’s the packing fraction for a simple cubic lattice.
There are two lattices that are described as close packed because they have the highest packing fraction of 0.74. They are the hexagonal close packed and the face centered cubic lattices.

Rather than stacking the baubles into a cube shape, they can be stacked into triangles, with the next layer of baubles sitting over the space in the centres of the triangles. If the third layer is directly over the first, we have a hexagonal close packed lattice. If the third layer sits over the gaps in the first and second then it’s a face centered cubic lattice. Let’s look at the hexagonal close packed lattice.
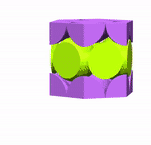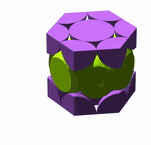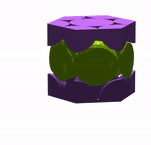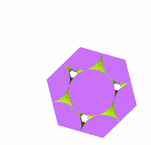
The hexagonal close packed lattice (HCP) is a little harder to analyse but can be analysed in the same way as the simple cubic lattice; i.e., we determine the number of spheres and thus the volume of all spheres in the repeated unit cell, and divide that by the volume of the unit cell, which in this case is a hexagonal prism. The stills below are taken from the animation.
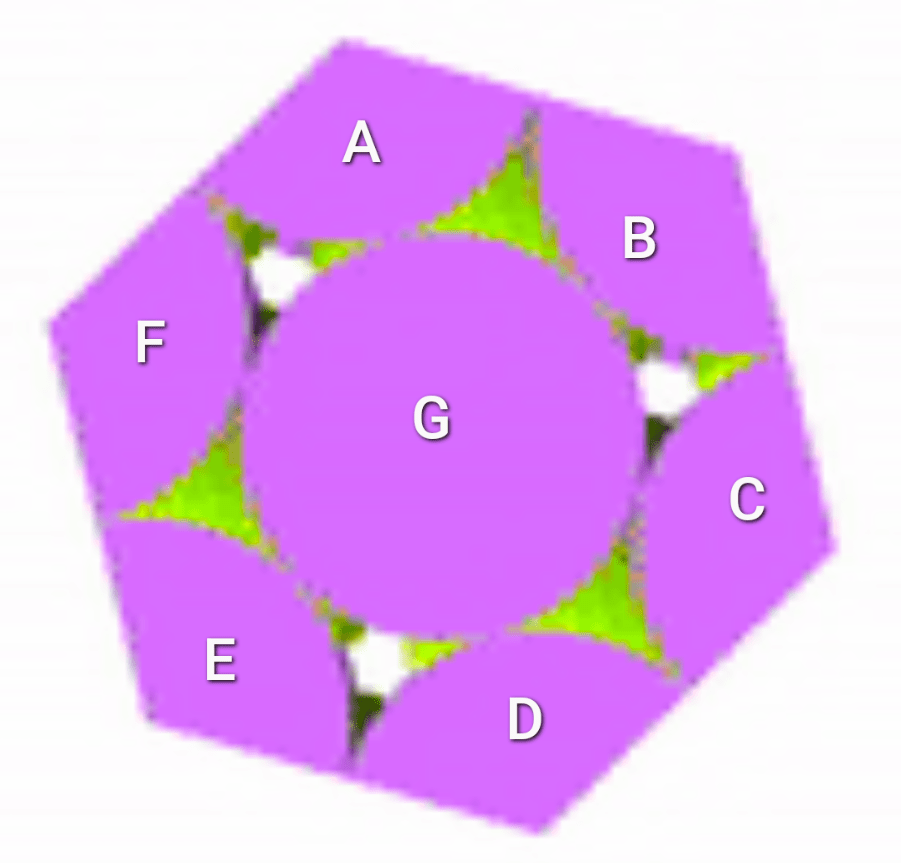
Let’s stick with the symbols from before: v is the volume of the sphere and V is the volume of the hexagonal prism. Here, A+B+C is half a sphere, D+E+F is half a sphere, and G is half a sphere. The top purple layer has a volume of 1.5×v; therefore, the two purple layers together have a volume of 3v. What of the green layer?

With the green layer, A+a is the volume of one green sphere, B+b is another, and C+c is another. So the volume of the green layer is 3v. Adding the green layer to the purple layer, the volume of filled space is 6v. So what of the hexagonal prism?
It can be shown that the volume of the hexagonal prism is V=24(√2)r³. The hexagonal prisms stack together like this:

The packing fraction v/V=[6×4πr³/3]/[24(√2)r³]=8π/(24(√2))=0.74 or 74%.
So the bottom line is, the shop I bought these from (Homebase) decided to stack the baubles in such a way that they could sell fewer baubles in the same space; how naughty.
Don’t forget!
GCSE live tuition is at 6pm tonight.
A-Level live tuition is at 7pm tonight.
